Evelin Trinidad Molina
Si buscas
hosting web,
dominios web,
correos empresariales o
crear páginas web gratis,
ingresa a
PaginaMX
Por otro lado, si buscas crear códigos qr online ingresa al Creador de Códigos QR más potente que existe


Fundamentos de las redes neuronales
La teoría y modelado de redes neuronales artificiales está inspirada en la estructura y funcionamiento de los sistemas nerviosos, donde la neurona es el elemento fundamental.
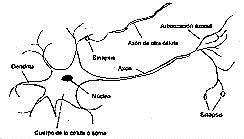
La neurona está formada por el cuerpo de la célula o soma, en donde se aloja el núcleo de la célula. Del cuerpo de la célula salen ramificaciones de diversas fibras conocidas como dendritas y sale también una fibra más larga denominada axón. Las dendritas se ramifican tejiendo una tupida red alrededor de la célula, mientras el axón se extiende generalmene un centímetro y en algunos casos hasta un metro. Este también se ramifica en filamentos y subfilamentos mediante los que establece conexión con las dendritas y los cuerpos de las células de otras neuronas. A esta conexión se la conoce con el nombre de sinapsis. Cada neurona puede establecer conexión desde con una docena de neuronas hasta con cientos de miles.
Las señales se propagan de una neurona a otra mediante una complicada reacción electroquímica. Las sinapsis liberan sustancias químicas transmisoras y entran a la dendrita, con lo cual se eleva el potencial eléctrico del cuerpo de la célula. Una vez que se rebasa un cierto límite, se envía al axón un impulso eléctrico o potencial de acción. El impulso se difunde a través de las ramas del axón llegando finalmente a las sinapsis y liberando transmisores en los cuerpos de otras neuronas. Las sinapsis que aumentan el potencial se conocen como excitadoras y las que lo disminuyen como inhibidoras. Una de las características más importantes de las conexiones sinápticas es la plasticidad: capacidad para alterar a largo plazo la intensidad de las conexiones como respuesta a un patrón de simulación. Las neuronas establecen también conexiones con otras neuronas y a veces con grupos de ellas capaces de migrar de un sitio a otro. Los mecanismos anteriores constituyen el fundamento del aprendizaje en el cerebro.
Conviene, para aclarar ideas, establecer una similitud directa entre la actividad sináptica y la actividad análoga en las redes neuronales artificiales: Las señales que llegan a la sinapsis son las entradas a la neurona; éstas son ponderadas (atenuadas o simplificadas) a través de un parámetro, denominado peso, asociado a la sinapsis correspondiente. Estas señales de entrada pueden excitar a la neurona o inhibirla (peso negativo). El efecto es la suma de las entradas ponderadas. Si la suma es igual o mayor que el umbral de la neurona, entonces esta se activa.
Elementos de una red neuronal artificial
Las redes neuronales artificiales (RNA) son modelos que intentan reproducir el comportamiento del cerebro.
Una RNA está constituida por nodos, o unidades, que están unidas mediante conexiones. Algunas de las unidades están conectadas al ambiente externo y se designan como unidades de entrada o de salida según reciban estímulos externos o den la respuesta del sistema, respectivamente. Hay otras unidades (neuronas) que simplemente están conectadas a otras neuronas del sistema y que al no tener relación directa con la información de entrada ni con la de salida del sistema, se denominan como unidades ocultas.Se conoce como capa o nivel a un conjunto de neuronas cuyas entradas provienen de la misma fuente ( que puede ser otra capa de neuronas) y cuyas salidas se dirigen al mismo destino (que puede ser otra capa de neuronas).
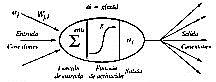
A cada conexión se le asigna un peso numérico, wji. Este constituye el principal recurso de memoria de largo plazo, y el aprendizaje usualmente se realiza con la actualización de tales pesos.
Además de las conexiones de entrada y de salida, cada neurona se caracteriza en cualquier instante por un valor numérico denominado estado o nivel de activación aj(t), cuyo cálculo está dividido en dos componentes, una lineal (función de entrada Netj) y otra no lineal (función de activación F).
La función de activación F, determina el nuevo estado de activación aj(t+1) de la neurona teniendo en cuenta la entrada total calculada, Netj, y el anterior estado de activación aj(t). Por lo general, todas las unidades de la red utilizan la misma función de activación.
aj(t+1) = F(aj(t), Netj)
En la mayoría de los casos, F es la función identidad, por lo que es estado de activación de una neurona en t+1 conicidirá con el Net de la misma en t. En este caso, el parámetro que se le pasa a la función de salida, f, de la neurona será directamente el Net. El estado de activación anterior no se tiene en cuenta. Según esto, la salida de una neurona j quedaría como
Netj = Sum (wji yi(t))
La función de salida fj, transforma el estado de activación actual en una señal de salida, yj. Dicha señal es enviada a través de las conexiones de salida a otras unidades de la red.
fj(aj(t)) = aj(t)
Existen tres funciones de transferencia típicas que determinan distintos tipos de neuronas:
Las señales se propagan de una neurona a otra mediante una complicada reacción electroquímica. Las sinapsis liberan sustancias químicas transmisoras y entran a la dendrita, con lo cual se eleva el potencial eléctrico del cuerpo de la célula. Una vez que se rebasa un cierto límite, se envía al axón un impulso eléctrico o potencial de acción. El impulso se difunde a través de las ramas del axón llegando finalmente a las sinapsis y liberando transmisores en los cuerpos de otras neuronas. Las sinapsis que aumentan el potencial se conocen como excitadoras y las que lo disminuyen como inhibidoras. Una de las características más importantes de las conexiones sinápticas es la plasticidad: capacidad para alterar a largo plazo la intensidad de las conexiones como respuesta a un patrón de simulación. Las neuronas establecen también conexiones con otras neuronas y a veces con grupos de ellas capaces de migrar de un sitio a otro. Los mecanismos anteriores constituyen el fundamento del aprendizaje en el cerebro.
Conviene, para aclarar ideas, establecer una similitud directa entre la actividad sináptica y la actividad análoga en las redes neuronales artificiales: Las señales que llegan a la sinapsis son las entradas a la neurona; éstas son ponderadas (atenuadas o simplificadas) a través de un parámetro, denominado peso, asociado a la sinapsis correspondiente. Estas señales de entrada pueden excitar a la neurona o inhibirla (peso negativo). El efecto es la suma de las entradas ponderadas. Si la suma es igual o mayor que el umbral de la neurona, entonces esta se activa.
Elementos de una red neuronal artificial
Las redes neuronales artificiales (RNA) son modelos que intentan reproducir el comportamiento del cerebro.
Una RNA está constituida por nodos, o unidades, que están unidas mediante conexiones. Algunas de las unidades están conectadas al ambiente externo y se designan como unidades de entrada o de salida según reciban estímulos externos o den la respuesta del sistema, respectivamente. Hay otras unidades (neuronas) que simplemente están conectadas a otras neuronas del sistema y que al no tener relación directa con la información de entrada ni con la de salida del sistema, se denominan como unidades ocultas.Se conoce como capa o nivel a un conjunto de neuronas cuyas entradas provienen de la misma fuente ( que puede ser otra capa de neuronas) y cuyas salidas se dirigen al mismo destino (que puede ser otra capa de neuronas).

A cada conexión se le asigna un peso numérico, wji. Este constituye el principal recurso de memoria de largo plazo, y el aprendizaje usualmente se realiza con la actualización de tales pesos.
Además de las conexiones de entrada y de salida, cada neurona se caracteriza en cualquier instante por un valor numérico denominado estado o nivel de activación aj(t), cuyo cálculo está dividido en dos componentes, una lineal (función de entrada Netj) y otra no lineal (función de activación F).
La función de activación F, determina el nuevo estado de activación aj(t+1) de la neurona teniendo en cuenta la entrada total calculada, Netj, y el anterior estado de activación aj(t). Por lo general, todas las unidades de la red utilizan la misma función de activación.
aj(t+1) = F(aj(t), Netj)
yj(t+1) = f(Netj)
La entrada calculada Netj se define como la suma ponderada de las salidas yn de las neuronas conectadas a la entrada y los pesos wn asociados a cada sinapsis.Netj = Sum (wji yi(t))
yj = fj(aj(t))
En algunos modelos, esta salida es igual al nivel de activación de la unidad, en cuyo caso la función fj es la función identidad.
fj(aj(t)) = aj(t)
- Función escalón : se utiliza cuando las salidas de la red son binarias. La salida de una neurona se activa sólo cuando el estado de activación es mayor o igual que cierto valor umbral t que representa la mínima entrada total ponderada necesaria para provocar la activación de la neurona.
- Función lineal : responde a las expresión f(x) = x. Se define un límite inferior -t y otro superior, t. Si la suma de las señales de entrada es menor que que -t, la activación se define como 0 o -1. Si la suma es mayor que t, la activación es 1. Para valores de entrada situada entre ambos límites, la activación se define como una función lineal de la suma de las señales de entrada.
- Función sigmoidal : es la más apropiada cuando se quiere como salida información analógica. Con esta función, para la mayoría de los valores del estímulo de entrada (variable independiente), el valor dado por la función es cercano a uno de los valores asintóticos. La importancia de esta función es que su derivada es siempre positiva y cercana a cero para los valores grandes positivos o negativos; además toma su valor máximo cuando x es 0. Esto hace que se puedan utilizar las reglas de aprendizaje en las cuales se usan derivadas. La expresión de esta función responde a la forma
Tu Sitio Web Gratis
© 2025 Evelin Trinidad Molina37219