Evelin Trinidad Molina
Si buscas
hosting web,
dominios web,
correos empresariales o
crear páginas web gratis,
ingresa a
PaginaMX
Por otro lado, si buscas crear códigos qr online ingresa al Creador de Códigos QR más potente que existe


MODELO DE NEURONA ARTIFICIAL
Se expone el modelo de una neurona de las Redes Neuronales Artificales (RNA). En primer lugar, se describe la estructura de una neurona artificial genérica, a continuación se muestra una versión simplificada de amplio uso en los modelos orientados a aplicaciones prácticas, que poseen una estructura más próxima a la neurona tipo clásica [Mc. Culloch-Pitts].
Aunque el comportamiento de algunos sistemas neuronales biológicos sea lineal, como sucede en la retina del cangrejo Limulus, en general, la respuesta de las neuronas biológicas es de tipo no lineal, característica que es emulada con las RNA desde la neurona formal original de Mc Culloch-Pitts.
La formulación de la neurona artificial como dispositivo no lineal constituye una de sus características más destacables, y una de las que proporciona un mayor interés a los RNA, pues el tratamiento de problemas altamente no lineales no suele ser fácil de abordar mediante técnicas convencionales.
Modelo general de neurona artificial.
Enseguida se describe la estructura genérica de neurona artificial en el marco establecido por el grupo PDP.
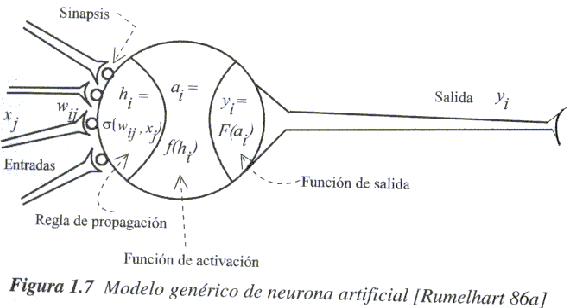
Se denomína procesador elemental o neurona, a un dispositivo simple de cálculo que, a partir de un vector de entrada procedente del exterior o de otras neuronas, proporciona una única respuesta o salida. Los elementos que constituyen la neurona de etiqueta "i" son los siguientes (véase la siguiente figura 1.7):
-
Conjunto de entradas,

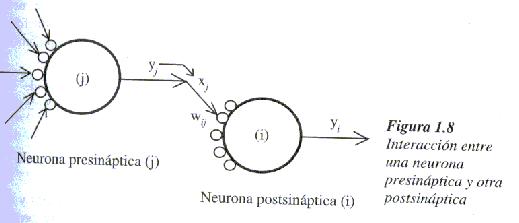
- Pesos sinápticos de la neurona i, wij~ que representan la intensidad de interacción entre cada neurona presináptica "j" y la neurona postsináptica "i".
-
Regla de propagación
 , que proporciona el valor del potencial postsináptico
, que proporciona el valor del potencial postsináptico  ,de la neurona "i" en función de sus pesos y entradas.
,de la neurona "i" en función de sus pesos y entradas. - Función de activación fi(ai(t-1), hi(t)), que proporciona el estado de activación actual ai(t) = fi ( ai (t-1), hi (t) ) de la neurona "i", en función de su estado anterior ai(t-1) y de su potencial postsináptico actual.
- Función de salida Fi (ai(t)), que proporciona la salida actual yi(t) = Fi (ai(t)) de la neurona "i" en función de su estado de activación.
La operación de la neurona "i" se expresa como sigue;
 (1.1)
(1.1)
Este modelo de neurona formal se inspira en la operación de la neurona biológica, en el sentido de integrar una serie de entradas y proporcionar cierta respuesta, que se propaga por el axón.
Las variables de entrada y salida son binarias (digitales) ó continuas (analógicas), dependiendo del modelo y su aplicación.
Por ejemplo, un perceptrón multicapa ó MLP (Multilayer Perceptron) admite ambos tipos de señales.
Así, para tareas de clasificación poseería salidas digitales (0,+1), mientras que para un problema de ajuste funcional de una aplicación multivariable continua, se utilizarían salidas continuas pertenecientes a un cierto intervalo.
Entradas y salidas
Dependiendo del tipo de salida, las neuronas suelen recibir nombres específicos. Así, las neuronas estándar cuya salida sólo puede tomar los valores "0" ó "1" se suelen denominar genéricamente neuronas de tipo Mc Culloch Pitts, mientras que aquellas que únicamente pueden tener por salidas ( -1 ó +1 ) se suelen denominar neuronas tipo Ising (debido al paralelismo con los modelos físicos de partículas con espín que adoptan únicamente dos estados, hacia arriba y hacia abajo).
Si adopta diversos valores discretos en la salida ( por ejemplo, -2, -1, 0, + 1, +2 ), se dice que se trata de una neurona de tipo Potts.
En ocasiones, el rango de los valores que una neurona de salida continua puede proporcionar se limita a un intervalo definido, por ejemplo, ( 0,+1 ) ó ( -1,+1 ).
Regla de propagación
La regla de propagación permite obtener, a partir de las entradas y los pesos, el valor del potencial postsináptico hi de la neurona;
 (1.2)
(1.2)
La función más habitual es de tipo lineal, y se basa en la suma ponderada de las entradas con los pesos sinápticos
 (1.3)
(1.3)
Formalmente se interpreta como el producto escalar de los vectores de entrada y pesos sinápticos.
 (1.4)
(1.4)
El peso sináptico wij define en la intensidad de interacción entre la neurona presináptica "j" y la postsináptica "i". Dada una entrada positiva (procedente de un sensor o simplemente la salida de otra neurona), si el peso es positivo tenderá a excitar a la neurona postsináptica, si el peso es negativo tenderá a inhibirla. Así se habla de sinapsis excitadoras (de peso positivo) e inhibidoras (de peso negativo).
Una regla de tipo no lineal, de uso más limitado, es la siguiente:
 (1.5)
(1.5)
Implica una interacción de tipo multiplicativo entre las entradas de la neurona (como se observa realmente en determinadas sinápsis biológicas).
El uso de esta última regla de propagación determina que una neurona se denomine de orden superior o neurona sigma-pi (por emplear sumas y productos), e implica una mayor complejidad, tanto en el estudio de la dinámica de la red neuronal, como en su realización hardware.
Otra regla de propagación habitual, especialmente en los modelos de RNA basados en el cálculo de distancias entre vectores (como RBF, mapas de Kohonen o LVQ), es la distancia euclídea
 (1.6)
(1.6)
Representa la distancia (al cuadrado) existente entre el vector de entradas y el de pesos. Cuando ambos vectores son muy similares, la distancia es muy pequeña; cuando son muy diferentes, la distancia crece.Por tanto, este tipo de regla opera de manera diferente a las anteriormente comentadas.
Se pueden utilizar también otros tipos de distancia, como la de Manhattan o la de Mahalanobis, que se abordarán más adelante.
Separar el concepto de regla de propagación y función de activación permite considerar desde un punto de vista unificado muchos modelos que de otra manera habría que tratar como casos especiales de una neurona estándar, (tal como sucede, por ejemplo, en el RBF o los mapas autoorganizados).
Función de activación ó función de transferencia
La función de activación ó de transferencia proporciona el estado de activación actual ai(t) a partir del potencial postsináptico hi(t) y del propio estado de activación anterior ai(t- 1)
 (1.7)
(1.7)
Sin embargo, en muchos modelos de sistemas neuronales artificiales ANS se considera que el estado actual de la neurona no depende de su estado anterior, sino únicamente del actual
 (1.8)
(1.8)
La función de activación f(.) se suele considerar determinista, y en la mayor parte de los modelos es monótona creciente y continua, como se observa habitualmente en las neuronas biológicas.
La forma y = f(x) de las funciones de activación más empleadas en los ANS se muestra en la tabla 1.1. Para abreviar, en ella designamos con "x" al potencial postsináptico, y con "y" el estado de activación.
La más simple de todas es la función identidad (que se puede generalizar al caso de una función lineal cualquiera), empleada, por ejemplo, en la Adalina.
Otro caso simple es la función escalón, empleada en el Perceptrón Simple y en la red de Hopfield discreta, así como en la neurona clásica de Mc Culloch-Pitts. La función lineal a tramos se puede considerar como una lineal saturada en sus extremos, es de gran sencillez computacional y resulta más plausible desde un punto de vista biológico pues, como se ha explicado, las neuronas se activan más a mayor excitación, hasta saturarse a la máxima respuesta que pueden proporcionar.
Los algoritmos de aprendizaje requieren que la función de activación cumpla la condición de ser derivable. Las más empleadas en este sentido son las funciones de tipo sigmoide, como la del BP.
Otra función clásica es la gaussiana, que se utiliza junto con reglas de propagación que involucran el cálculo de cuadrados de distancias (por ejemplo, la euclídea) entre los vectores de entradas y pesos.
Por último, en ocasiones se emplean funciones sinusoidales, como en aquellos casos en los que se requiere expresar explícitamente una periodicidad temporal.
Función de salida
Esta función proporciona la salida global de la neurona yi(t) en función de su estado de activación actual ai(t). Muy frecuentemente la función de salida es simplemente la identidad F(x)=x, de modo que el estado de activación de la neurona se considera como la propia salida;
 (1.9)
(1.9)
Esto ocurre en los modelos más comunes, como el MLP o la adalina. La función de salida es de tipo escalón, lo que supone que la neurona no se dispare hasta que la activación supere un cierto umbral. En otros modelos, como es el caso de la máquina de Boltzmann, se trata de una función estocástica de la activación, con lo que la neurona tendrá un comportamiento probabilístico.
Este modelo de neurona formal se inspira en la operación de la neurona biológica, en el sentido de integrar una serie de entradas y proporcionar cierta respuesta, que se propaga por el axón.
Las variables de entrada y salida son binarias (digitales) ó continuas (analógicas), dependiendo del modelo y su aplicación.
Por ejemplo, un perceptrón multicapa ó MLP (Multilayer Perceptron) admite ambos tipos de señales.
Así, para tareas de clasificación poseería salidas digitales (0,+1), mientras que para un problema de ajuste funcional de una aplicación multivariable continua, se utilizarían salidas continuas pertenecientes a un cierto intervalo.
Entradas y salidas
Dependiendo del tipo de salida, las neuronas suelen recibir nombres específicos. Así, las neuronas estándar cuya salida sólo puede tomar los valores "0" ó "1" se suelen denominar genéricamente neuronas de tipo Mc Culloch Pitts, mientras que aquellas que únicamente pueden tener por salidas ( -1 ó +1 ) se suelen denominar neuronas tipo Ising (debido al paralelismo con los modelos físicos de partículas con espín que adoptan únicamente dos estados, hacia arriba y hacia abajo).
Si adopta diversos valores discretos en la salida ( por ejemplo, -2, -1, 0, + 1, +2 ), se dice que se trata de una neurona de tipo Potts.
En ocasiones, el rango de los valores que una neurona de salida continua puede proporcionar se limita a un intervalo definido, por ejemplo, ( 0,+1 ) ó ( -1,+1 ).
Regla de propagación
La regla de propagación permite obtener, a partir de las entradas y los pesos, el valor del potencial postsináptico hi de la neurona;
La función más habitual es de tipo lineal, y se basa en la suma ponderada de las entradas con los pesos sinápticos
Formalmente se interpreta como el producto escalar de los vectores de entrada y pesos sinápticos.
El peso sináptico wij define en la intensidad de interacción entre la neurona presináptica "j" y la postsináptica "i". Dada una entrada positiva (procedente de un sensor o simplemente la salida de otra neurona), si el peso es positivo tenderá a excitar a la neurona postsináptica, si el peso es negativo tenderá a inhibirla. Así se habla de sinapsis excitadoras (de peso positivo) e inhibidoras (de peso negativo).
Una regla de tipo no lineal, de uso más limitado, es la siguiente:
Implica una interacción de tipo multiplicativo entre las entradas de la neurona (como se observa realmente en determinadas sinápsis biológicas).
El uso de esta última regla de propagación determina que una neurona se denomine de orden superior o neurona sigma-pi (por emplear sumas y productos), e implica una mayor complejidad, tanto en el estudio de la dinámica de la red neuronal, como en su realización hardware.
Otra regla de propagación habitual, especialmente en los modelos de RNA basados en el cálculo de distancias entre vectores (como RBF, mapas de Kohonen o LVQ), es la distancia euclídea
Representa la distancia (al cuadrado) existente entre el vector de entradas y el de pesos. Cuando ambos vectores son muy similares, la distancia es muy pequeña; cuando son muy diferentes, la distancia crece.Por tanto, este tipo de regla opera de manera diferente a las anteriormente comentadas.
Se pueden utilizar también otros tipos de distancia, como la de Manhattan o la de Mahalanobis, que se abordarán más adelante.
Separar el concepto de regla de propagación y función de activación permite considerar desde un punto de vista unificado muchos modelos que de otra manera habría que tratar como casos especiales de una neurona estándar, (tal como sucede, por ejemplo, en el RBF o los mapas autoorganizados).
Función de activación ó función de transferencia
La función de activación ó de transferencia proporciona el estado de activación actual ai(t) a partir del potencial postsináptico hi(t) y del propio estado de activación anterior ai(t- 1)
Sin embargo, en muchos modelos de sistemas neuronales artificiales ANS se considera que el estado actual de la neurona no depende de su estado anterior, sino únicamente del actual
La función de activación f(.) se suele considerar determinista, y en la mayor parte de los modelos es monótona creciente y continua, como se observa habitualmente en las neuronas biológicas.
La forma y = f(x) de las funciones de activación más empleadas en los ANS se muestra en la tabla 1.1. Para abreviar, en ella designamos con "x" al potencial postsináptico, y con "y" el estado de activación.
La más simple de todas es la función identidad (que se puede generalizar al caso de una función lineal cualquiera), empleada, por ejemplo, en la Adalina.
Otro caso simple es la función escalón, empleada en el Perceptrón Simple y en la red de Hopfield discreta, así como en la neurona clásica de Mc Culloch-Pitts. La función lineal a tramos se puede considerar como una lineal saturada en sus extremos, es de gran sencillez computacional y resulta más plausible desde un punto de vista biológico pues, como se ha explicado, las neuronas se activan más a mayor excitación, hasta saturarse a la máxima respuesta que pueden proporcionar.
Los algoritmos de aprendizaje requieren que la función de activación cumpla la condición de ser derivable. Las más empleadas en este sentido son las funciones de tipo sigmoide, como la del BP.
Otra función clásica es la gaussiana, que se utiliza junto con reglas de propagación que involucran el cálculo de cuadrados de distancias (por ejemplo, la euclídea) entre los vectores de entradas y pesos.
Por último, en ocasiones se emplean funciones sinusoidales, como en aquellos casos en los que se requiere expresar explícitamente una periodicidad temporal.
Función de salida
Esta función proporciona la salida global de la neurona yi(t) en función de su estado de activación actual ai(t). Muy frecuentemente la función de salida es simplemente la identidad F(x)=x, de modo que el estado de activación de la neurona se considera como la propia salida;
Esto ocurre en los modelos más comunes, como el MLP o la adalina. La función de salida es de tipo escalón, lo que supone que la neurona no se dispare hasta que la activación supere un cierto umbral. En otros modelos, como es el caso de la máquina de Boltzmann, se trata de una función estocástica de la activación, con lo que la neurona tendrá un comportamiento probabilístico.
Tu Sitio Web Gratis
© 2025 Evelin Trinidad Molina37201